Settepercento | Three Body Problem

made easy

The three-body problem is not only the title of a series of books first and of a TV series now, but it is one of the most intricate and fascinating challenges of past and contemporary physics and astronomy.

The formulation of the problem is apparently very simple: given the initial position, mass and velocity of three celestial bodies, is it possible to describe the evolution of their respective orbits over time?

But in the vast theater of deep space, where gravitational forces intertwine the destinies of the planets, nothing is as "simple" as it appears.

The reason for this acceleration/deceleration is that the two bodies are subject to the influence of mutual gravitational attraction, which acts in a proportional manner with respect to their mass and their distance, as discovered by Isaac Newton in his law of universal gravitation.

As the planet moves away from the Sun, the gravitational force decreases and the acceleration decreases accordingly.

This is the main basic dynamics of the movement of celestial bodies in space and this alone is enough for us to start complicating things and getting to the core of the famous problem. Ultimately, the evolution of an Earth-Sun system, given the low mobility of the latter, can be seen as a "1-body problem”.

These, as seen in the previous example, attract and repel each other due to gravity.

Can the future evolution of such a composed system be calculated? The answer is yes, and doing so means writing a series of differential equations capable of describing the future motion of the two bodies starting from their positions and speed. These equations, which are apparently also quite complex, are all in all solvable in closed form and fully understandable by experts.

But if we complicate the system by adding just one more celestial body, the calculations suddenly go wrong. This is the scenario of the famous three body problem, and unfortunately for us from here on things start to get very complicated.

But don't worry, let's take a step back and try to proceed in an orderly way.

To predict the configuration of a 3-body system over time, in a completely analogous way to the 2-body problem, we must imagine being able to write a mathematical formula capable of explaining the value of the position and momentum of the three bodies at every instant of time.

Ideally this formula should work for all possible starting configurations of the three bodies and must be able to be resolved with a finite number of mathematical operations.
So let's look at the system closely and try to describe what happens.

Now knowing some rudiments of the movement of the planets, we know that neighbors A and B, exerting the gravitational force, attract each other. So far everything is normal. We are in the problem of 2 bodies, so we are perfectly capable of describing and calculating their movements over time... except that C, the farthest of the three, attracts both A and B. So we will have to redo all the calculations for this reason.

But A also exerts a force on C and this changes things, so let's readjust the calculations. Wait… B also pushes on C, so we have to recalculate again.
But it doesn't end here. The new configuration affects how C pulls on A and B, which in turn changes how A push on B and C which changes how B exerts gravitational pull on A and C. All while everyone and three advance along their respective orbit. Basically we have to recalculate again, again and again...

In short, as you have understood, increasing even just a single degree of freedom in the system causes an exponential increase in possible configurations, to the point that it becomes practically impossible to resolve a 3-body state in a closed form due to the mathematical complexity that originates.

To better understand this complexity, imagine a two-body system like tossing a coin. There are only two possible outcomes: heads or tails. The analogue of the 3-body system might be to roll three dice. There are 6 possible outcomes for each dice and the total number of combinations is 216. Quite a difference, right?

Obviously, both the two-body and three-body problems represent hypothetical situations designed to understand the principles of orbital mechanics and are only starting points for many calculations in space exploration and satellite dynamics.

In reality, there are gravitational interactions by so many different celestial bodies that are far more complex than those described, to the point that we come to speak of the problem of n-bodies. It will not surprise you that these systems are framed within what is called "chaos theory".

If there is no way to predict the movements of this system then how does NASA, for example, make predictions about comets or to calculate the trajectories of the satellites it sends into orbit? After all, aren't those also part of the 3 or more bodies problem?
Yes that’s true, and a possible solution to the chaos exists. But to understand it we must leave the realm of analytical mathematics and embrace the world of numerical integration and of probability, accepting the possibility of making some mistakes.

The process used to predict the orbits of a chaotic system is based on the capabilities of modern computing units to simulate reality taking into account all assigned constraints. In fact, once the simulation parameters have been defined, we are able to generate small finite segments of approximate orbits of a 3-body system.

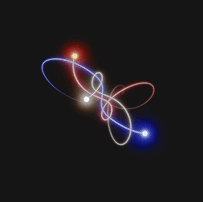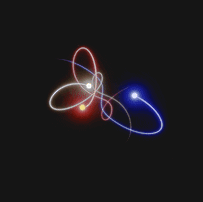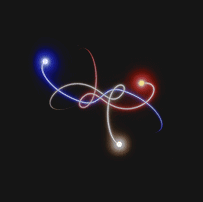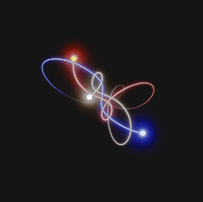
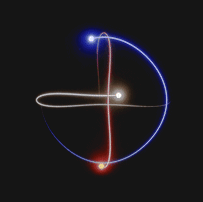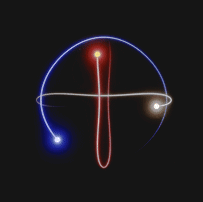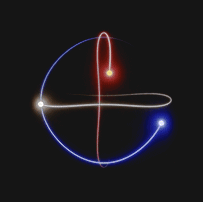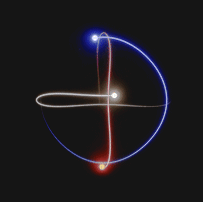
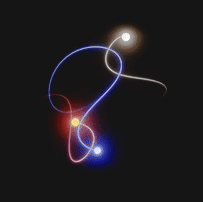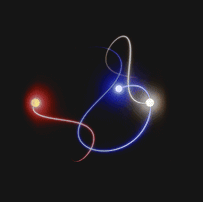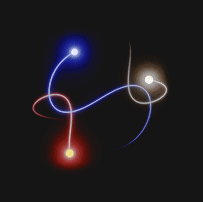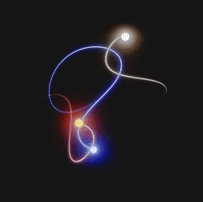
Approximate solutions are calculated at each instant of time. In fact, for each instant of time, there is a numerical value associated with the position and momentum, which is used to calculate the solution at the next time step.

The simulation-statistical approach is an essential tool for planning space missions. Even if the answer to the problem can never be precise, it can be very accurate, especially if we extend the execution time by a lot. At least as long as the brute force of our CPUs can resist. But can having a structurally "inaccurate" solution to a system that is already so incredibly unstable bring some kind of catastrophic consequence?

It’s difficult to answer this question, but there are at least two situations that could be negatively affected by this approximation error.

…Unless a planet that previously followed a stable orbit suddenly decides to change its trajectory, throwing our predictions out of whack, with the risk of throwing the Earth into what would be a real Age of Chaos.

That said, there's probably nothing to worry about. Ultimately, the problem of the three bodies, behind its apparent simplicity, gives us the opportunity to reflect on our limits and to appreciate the complexity of the nature of the universe, reminding us that all in all, quoting the best seller by Liu Cixin, we're almost like of insects, watching helplessly and fascinated by the spectacular circling of celestial bodies above their heads..

Congrats

You have reached the end of the article in